|
|
|
|
Alternate View Column AV-18
Keywords: centrifugal, Coriolis, force,
artificial gravity, rotation, space station
Published in the February-1987 issue of
Analog Science Fiction & Fact Magazine;
This column was written and submitted 8/1/86 and is copyrighted
©1986, John G. Cramer. All rights reserved.
No part may be reproduced in any form without
the explicit permission of the author.
The space station doughnut of 2001 and the O'Neill space-habitat cylinder have become part of the furniture of science fiction, so much so that we take spin-generated artificial gravity to be interchangeable with the Earth-normal variety in which we live. But there are differences that would be quite apparent to anyone living in the spin-generated variety. The subject of this AV column is an exploration of the differences between the "natural" gravity of Earth and the "artificial" gravity of a rotating space station.
My interest in the physics of space station gravity developed because last year Vonda McIntyre was writing a book with a space station setting, and she asked my advice. The book, Barbary, is about a teenager who leaves Earth to live in a space station with spin-generated gravity. I helped Vonda in a very minor way by identifying the physical effects that the heroine would experience in that environment. What's it like to ride an elevator in a space station? How would a ball game look if it were played there? If you woke up in a strange location, what simple tests would tell if you were in a rotating space station rather than at rest on the ground? And so on ... I found that there are some interesting side-effects of artificial gravity, perhaps well known to NASA experts but obscure to the rest of us. And I was surprised to find that some recent SF hasn't been too accurate in describing the space habitat environment.
Looking at the world from a rotating vantage point (be it a merry-go-round or a space station) is odd and confusing. So let's start with a simple concrete example. Suppose that we are on a doughnut space station, about half the size of the big one in 2001, providing living and working space at earth-normal gravity (1 g) for about 150 people. Such a station might take the form of a "wheel" 15 m wide and 160 m in diameter, rotating on its axis so that it makes a full rotation every 18 seconds. Because the floor of the space station rotates through it's full circumference in this time, it has a speed (called the tangential velocity because the velocity lies along the tangent of the circle of travel) of 27.9 m/s. A note here on scaling to other sizes: If the station had 4 times this diameter, the rotation period to give 1 g of artificial gravity would be twice as long and the speed of the floor would be twice as large.
Let's do a simple "Mr. Science" experiment in this space station. Place a phonograph turntable on floor and use it to spin a cake pan filled with water. Let's use a cake pan 40 cm in diameter and spin it at the 78 RPM setting of the turntable. The outer edges of the spinning cake pan will be moving at a speed of 1.6 m/s with respect to the floor. Therefore, the edge of the cake pan towards one outside wall of the station is traveling at an absolute speed of (27.9+1.6)=29.5 m/s, while the opposite edge of the pan has a speed of (27.9-1.6)=26.3 m/s. The pull of artificial gravity depends on the square of this tangential speed, so the "fast" edge experiences an increased pull of 1.12 g, while the pull on the "slow" edge decreases to 0.89 g. The water in the pan will tend to tilt, climbing higher on the slow edge and dropping lower on the fast edge. A spinning gyroscope would tumble in the same way, making the toy top a poor gift for a space child. And so we see different physical effects in the artificial gravity of a space station than would be found if the same experiments were performed in the "natural" gravity of Earth.
This simple experiment has an interesting implication for the psycho-physiology of human balance. Our equilibrium and our perception of vertical orientation come from the interaction of the fluid in the semicircular canals of our inner ears with the nerve fibers there. The vertigo experienced during and after spinning in an amusement park ride demonstrates what happens when this mechanism is disturbed. Seasickness is another example. Now suppose that you stand looking spinward down the long upward-curving hall along the rim of the space station, and then rapidly turn your head clockwise so that you are looking at the side wall to your right. Your head has made a rotation similar to that of the pan on the turntable. The fluid in your semicircular canals will therefore rise on one side and drop on the other as the water did. The subjective consequence is that you will "see" the floor tilt to the left, with the right side wall "rising" and the left side wall "dropping" momentarily. The amount of perceived floor tilt depends on the ratio of ear-velocity to floor velocity, but for any but the very largest of space stations the tilt sensation will be a quite unmistakable. This effect is likely to be fairly disorienting and may be a source of nausea and vertigo for the "greenhorn" who has just arrived from "natural" gravity. For the experienced space station inhabitant, however, the "floor-tilt effect" will become a useful aid to orientation because it will allows the user to tell whether he is looking "spinward" (in the direction that the floor is moving due to the spin) or "anti-spinward" (against the floor velocity) down the hall.
Head twisting and nodding will also produce other subjective effects. Facing a wall at right angles to the spin direction and doing a similar head twist will make the floor seem to tilt up or down. Nodding or wobbling your head will produce similar effects. Placed in a small closed room, the experienced space station dweller can establish his orientation with respect to the spin of the station with a few twists of his head.
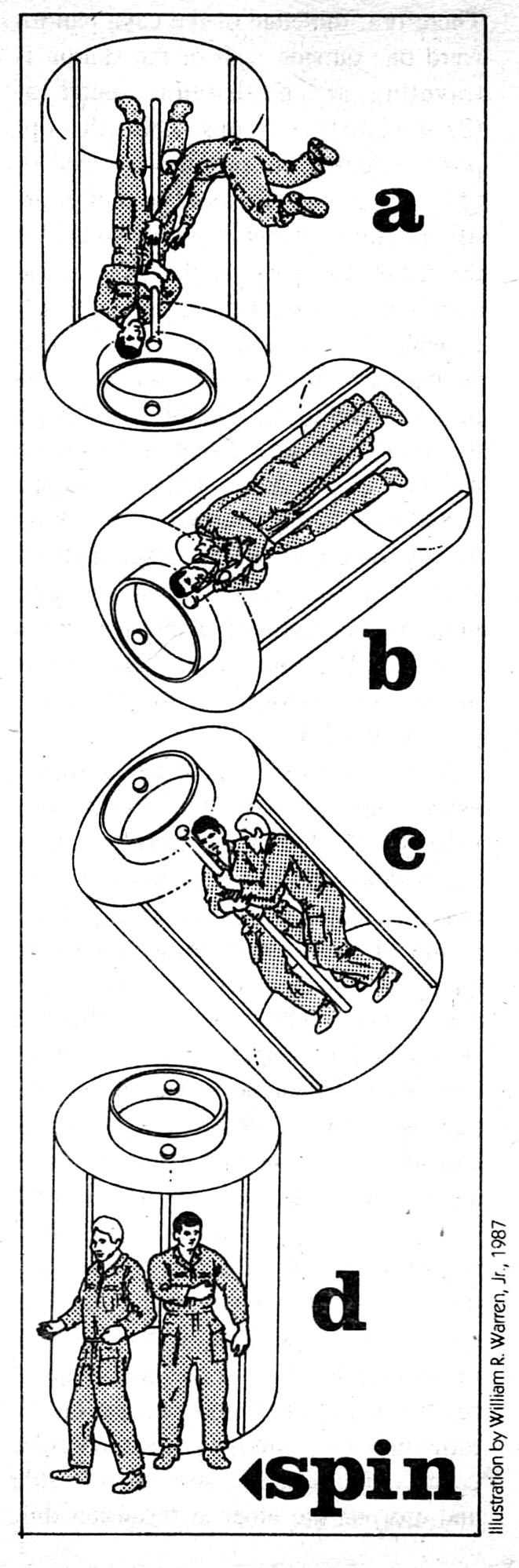 The memorable jogging scene of 2001 when astronaut Frank Poole runs in
what we see as a vertical circle brings to mind another effect. The jogger
running spinward down a hall along the rim of the station increases his
tangential velocity, thereby creating a slight increase in the centrifugal pull
he experiences and giving the impression of running uphill. Running
anti-spinward will decrease the pull slightly and create the impression of
running downhill. The change in pull will depend on the ratio of running speed
to floor speed, and the effect would be less in a big station than a small
one.
The memorable jogging scene of 2001 when astronaut Frank Poole runs in
what we see as a vertical circle brings to mind another effect. The jogger
running spinward down a hall along the rim of the station increases his
tangential velocity, thereby creating a slight increase in the centrifugal pull
he experiences and giving the impression of running uphill. Running
anti-spinward will decrease the pull slightly and create the impression of
running downhill. The change in pull will depend on the ratio of running speed
to floor speed, and the effect would be less in a big station than a small
one.
The mysterious "force" that makes the water tilt in the pan, moves the fluid in the semicircular canals, and changes the pull on the runner is called the Coriolis force. Like the "centrifugal force" which makes spin-generated artificial gravity, the Coriolis force is not a real force of nature, but rather a sort of illusion or pseudo-force which appears to observers in rotating systems. But if the Coriolis force is an illusion, its effects are nevertheless quite real. Its actions on air flow on the Earth's surface are responsible for the circular weather patterns visible in satellite weather pictures: the ragged spiral of the hurricane and the gentle swirl and counter-swirl of high and low pressure areas.
Another Coriolis effect appears when we ride the space station's elevator. There are good astronautical engineering reasons for arranging the station so that arriving shuttles dock at the station hub, matching velocity and spin with the station before establishing tight mechanical contact. Arriving passengers exit the shuttle in the zero-gravity zone of the hub and then ride an elevator to the 1 g zone at the rim where the living and working areas are located. But what is the elevator ride like? The elevator must travel 80 m from hub to rim, the rough equivalent of the elevator in a 25 story building. Let's assume that the elevator is set to accelerate to a speed of 5 m/s in a period of 2 seconds, then travel toward the rim at that speed for 14 seconds, and finally decelerate to zero velocity in the final 2 seconds of the trip.
With this arrangement, the elevator riders will be pushed against the ceiling of the car for two second with a force of 0.25 g. During that 2 second period a pull toward the anti-spinward wall of the car will build up to a force of 0.22 g. During the 14 second ride this sideways force will remain constant, but added to it will be a downward force which builds up to 1 g as the centrifugal force of the station's spin builds. Finally in the last 2 seconds of the ride the downward force will rise to 1.25 g and the pull toward the anti-spinward wall will diminish to zero. As the car stops and the passengers step out the constant 1 g downward pull of the station is all that remains. And so the passengers have had a very peculiar ride. Their perception of "down-ness" has migrated from the ceiling to the anti-spinward wall and finally to the floor, as if the car had rotated 180o during the trip.
The source of the sideways pull in the elevator is the Coriolis force. An equivalent view is that the riders in the elevator must travel from the hub, where they have zero tangential velocity, to the rim, where they must match the 27.9 m/s tangential velocity of the floor. Clearly during the elevator ride they must not only be taken "down" along a radius from the hub to the rim, but they must also be accelerated up to the speed of their new environment. The sideways push of the elevator wall accomplishes this. A similar ride in the upward direction from rim to hub would reverse these forces, and now the sideways pull toward the spinward wall removes the rim's tangential speed to match the hub environment.
Finally, let's consider space station sports. How would a baseball pitch or a
basketball pass be changed in the environment of the space station? The answer
depends on the direction of travel of the ball. Movement parallel to the
station's axis of rotation, across the long hallway for example, shows no
Coriolis effects. But a ball thrown spinward will seem to drop, and an
anti-spinward pitch will rise due to Coriolis effects. Similarly a falling
object will curve antispinward, a rising object will curve spinward due to the
Coriolis effects, as we saw in the case of the descending elevator. Athletes
after sufficient practice will begin to view these distortions of trajectory as
natural and will automatically include compensations for them as a part of
optimum performance. However, the size of the compensations needed depends on
the tangential velocity of the space station floor, with higher velocities
leading to smaller Coriolis effects. In an Inter-Orbital Olympics where
participants from a variety of stations of different sizes are assembled for
athletic competition there will be a definite "home-court" advantage.
Participants from smaller-diameter space stations will tend to overcorrect for
the Coriolis effects and participants from larger diameter stations will
undercorrect. I wonder how the Inter-Orbital Olympic Committee will handle
that one?
John G. Cramer's 2016 nonfiction book (Amazon gives it 5 stars) describing his transactional interpretation of quantum mechanics, The Quantum Handshake - Entanglement, Nonlocality, and Transactions, (Springer, January-2016) is available online as a hardcover or eBook at: http://www.springer.com/gp/book/9783319246406 or https://www.amazon.com/dp/3319246402.
SF Novels by John Cramer: Printed editions of John's hard SF novels Twistor and Einstein's Bridge are available from Amazon at https://www.amazon.com/Twistor-John-Cramer/dp/048680450X and https://www.amazon.com/EINSTEINS-BRIDGE-H-John-Cramer/dp/0380975106. His new novel, Fermi's Question may be coming soon.
Alternate View Columns Online: Electronic reprints of 212 or more "The Alternate View" columns by John G. Cramer published in Analog between 1984 and the present are currently available online at: http://www.npl.washington.edu/av .
Reference:
Spin Generated Gravity:
"An Overview of Artificial Gravity", R. W. Stone, Jr., NASA Report SP-314 (1973).
|
|
|
|
This page was created by John G. Cramer on 7/12/96.