Consider
this: The ship descended silently on its
antigravity drive until it hovered a few centimeters above the surface of the
airless planet. The astronaut in his bulky suit climbed ponderously down the
ladder, carrying the flag of the United Federation of Planets in one hand. As he
stepped out over the surface of the planet, he began to recite the ritual
phrase,
"Thatís one small step for a man, andÖ" His foot made contact
with the planet.
Finally
the ball of radioactivefire thinned enough to make it possible to see the place
where the ship had been. An enormous new crater, still glowing with
incandescence at the center, now scarred the surface of the antiplanet. Man had
found antimatter.
It could happen someday. But where is the antimatter? We know that antimatter can be made in the laboratory. Using accelerated particles or gamma rays with enough energy, we can make electrons and positrons (antimatter electrons) in pairs. With more energy we can make proton-antiproton pairs or neutron-antineutron pairs. Notice that in these processes we must always make a matter particle along with the antimatter particle. When the matter around us was made (perhaps in the Big Bang) some antimatter should have been made at the same time. So why do we see no antimatter in nature, not even in cosmic rays? Where can it be hiding? Are there antimatter meteors? Anti-planets? Anti-stars? Anti-galaxies? Are there antimatter life-forms? Anti-people? Anti-civilizations?
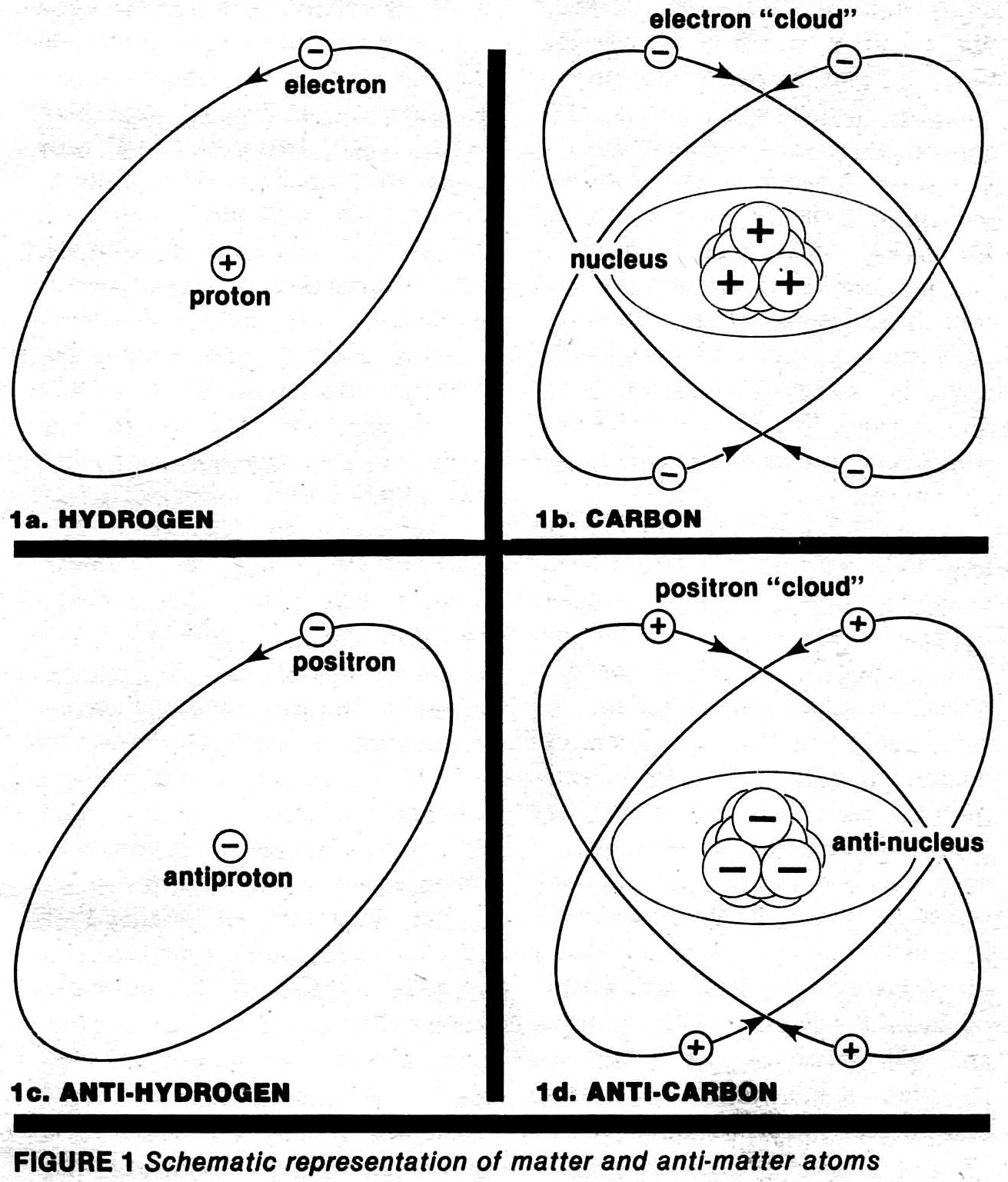
To understand the full implications of these questions we must first understand what antimatter is and how it relates to ordinary garden variety matter. Fig. la shows a schematic view of an atom of ordinary hydrogen, the simplest atom of all. A hydrogen atom has a positively charged proton at its "nucleus" at the center (like a sun in a solar system) and a negatively charged electron orbiting around the proton (like a planet around the sun). The charge of the electron is equal and opposite that of the proton, but the mass of the electron is only l/1836 of the protonís mass (for comparison, Jupiter has 1/1047 of the sunís mass). Fig. lb shows carbon-12, a somewhat more typical atom. It has 6 protons and 6 neutrons in its nucleus and a "cloud" of 6 electrons in orbit.
In the corresponding "antihydrogen" atom (Fig. lc), the central proton is replaced by an antiproton with the same mass as a proton but with a negative electric charge. The electron is replaced by a positron with the same mass as an electron with a positive charge. Fig. ld shows an "anticarbon" atom with 6 antiprotons and 6 antineutrons in the nucleus (charge -6) and 6 positrons in the "cloud" (charge +6). These atoms behave the same way as normal hydrogen and carbon, have the same masses, the same chemical properties, the same excited states, resonances, and atomic structure, but the charge of the nucleus is negative and the "cloud" contains positively charged positrons instead of electrons. If the antimatter atoms are completely isolated, their behavior is identical in every way to the equivalent matter atoms. If, however, we place antimatter atoms next to atoms of normal matter, they destroy each other and release a large amount of energy in a 54 process called annihilation, which is a spectacularly different story.
Fig. 2a illustrates what happens when an electron and a positron get together. Their annihilation is a miniature explosion in which the charges of the electron and positron cancel, and their combined mass energy (about 1 million electron volts or l MeV) is released. Since there are no lighter charged particles to get into the act, this energy is converted into electromagnetic radiation, in the form of a pair of gamma rays (high energy light photons) emitted in opposite directions.
The annihilation of a proton with an antiproton is shown in Fig. 2b. Here the situation is more complicated because there are several kinds of lighter charged particles (pions, muons, and electrons) that can participate. What happens is not nearly as simple as the emission of a pair of back-to-back gamma rays. Instead, about one-third of the time the proton-antiproton annihilation produces a pi-zero meson and two gamma rays, and the other two-thirds of the time a charged (+ or -) pion, a muon (- or +) and a neutrino are produced. I will not dwell on all the games that the pions and muons play, but they are unstable particles that promptly break down into electrons and positrons, photons and neutrinos.
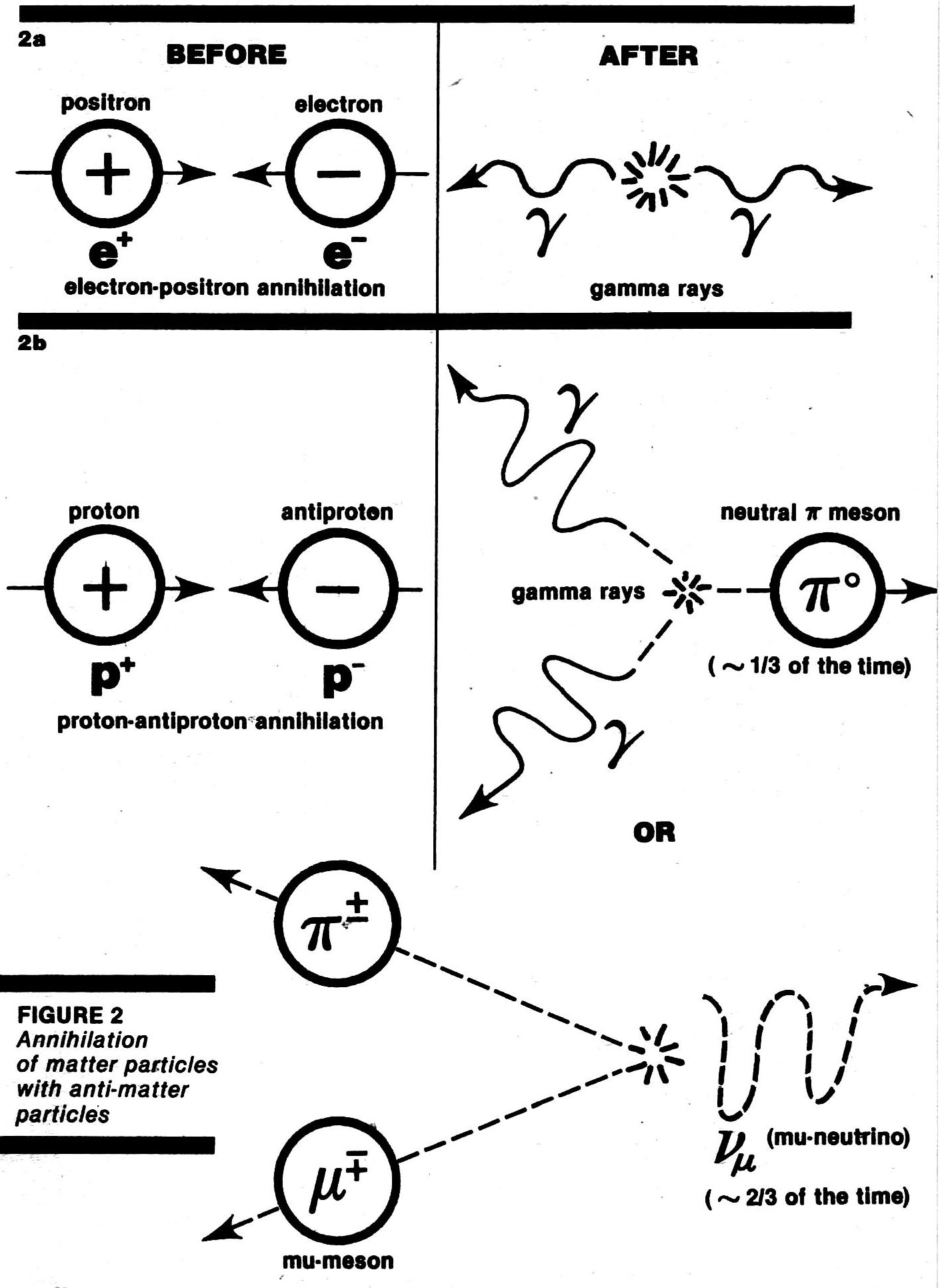
Of the mass-energy released in the proton-antiproton annihilation (1,877 MeV), about half ends up as neutrinos, one-third as gamma rays, and one-sixth as energetic electrons and positrons. The energy that goes into gamma rays and electrons is delivered to the surrounding material, if there is any, through electromagnetic interactions. The neutrino energy is effectively lost since the neutrino is not electrically charged, travels at the speed of light, and can pass through light-years of lead or concrete without being stopped or scattered.
If larger atoms of matter and antimatter (say carbon + anticarbon) should come into contact, more complicated events can occur, but the result is essentially the same: the total mass of the atom plus antiatom is completely converted into energy, about half in the form of energetic neutrinos and the rest in the form of energetic particles that interact electromagnetically. Here then is the solution to the worldís energy problems. Here is energy in its most concentrated form: mass; mass that can be readily converted to energy by annihilation. Small, compact, simple, direct conversion of mass to energy is the realization of Einsteinís famous equation E=mc2. What more could you want? As it turns out, you could want a lot more.
There are some very formidable (and potentially very dangerous) problems associated with handling antimatter. Suppose someone were to present you with a cube of antimatter one centimeter on a side (or about the size of a sugar cube). If this cube had approximately the density of water, its complete annihilation would produce about 50,000,000 kilowatt-hours of energy (half of it useable). But what would you do with it? You canít hold it in your hand or grab it with tongs or put it down on any surface. It will annihilate with whatever matter it touches and will release enough energy and radiation to kill you, leaving a large crater where you were standing.
Suppose you dropped the antimatter cube: would it fall down or up? You might be tempted to think that since antimatter has a reversed electrical charge, it will also have a reversed gravitational "charge" (which is called negative gravitational mass) and will be pushed away from the Earth by gravity. However, we know from experimental evidence plus the Equivalence Principle from Einsteinís general theory of relativity that this is not the case. Antiprotons and positrons are found experimentally to behave quite normally in terms of their inertial mass. A force pushing an antiproton to the right will cause it to accelerate to the right, so its inertial mass is normal. The Equivalence Principle equates inertial mass with gravitational mass, so antimatter particles must also have positive gravitational mass and be attracted toward the Earth by gravity. So you must find a way of supporting your antimatter chunk to keep it from falling downward (not upward). You will have to levitate it using only electric and magnetic fields to insure that there is no physical contact.
There are several ways in which you can do this. If the antimatter material is a reasonable electrical conductor you can use a rapidly varying magnetic field, the antimatter floating on its own induced magnetic field produced by eddy currents. If the antimatter material is a reasonable dielectric (like glass) a rapidly varying electric field can be used to support it. Further, if the chunk of antimatter is hot, (as we will see, it is likely to be) it will probably acquire a negative electrical charge as it "boils off " positrons (just as the hot cathode of a-vacuum tube boils off electrons). Therefore it could be suspended with static electrical forces between a pair of electrically charged plates, the positive plate above the sample and the negative plate below. So in one "way or another you can keep your cube floating in mid-air, supported only by electromagnetic forces and not physically contacting any surface made of normal matter. Unfortunately, this does not prevent all contact with matter.
There still remains the problem of contact with gas molecules. If you were to attempt to keep the antimatter cube in air, it would literally explode like a bomb because of the energy released by annihilation with air molecules. Now suppose that you place it in a relatively good vacuum, say 10-6 torr (about one-billionth of atmospheric pressure). At this pressure the annihilation of the cube with the residual gas molecules present in the vacuum would release energy at the rate of about 20 million joules per second or 20 megawatts, about the output of a small power plant. This energy would be mostly in the form of energetic gamma rays. It would be quite lethal to anyone within about a mile of it.
You could make the vacuum better, say 10-9 torr. The rate of energy release would then be only 20 kilowatts. If the vacuum was made really superb, say 10-11 torr, then only about 200 watts of annihilation energy would be dissipated or about the equivalent of two light bulbs. This seems to be a modest power level, but you must remember that this is 200 watts of energetic gamma rays, not heat. That is enough radiation to make your white corpuscles roll over on their backs and put their little legs in the air. You are making gamma rays with an average energy of about 200 MeV each, about 2 trillion of them per second. Clearly, even if your chunk of antimatter is levitated and placed in a superb vacuum, it would still be an enormous radiation hazard and would have to be shielded with very large slabs of lead or concrete.
On the other hand, we do have the makings of a power plant. All we have to do is contain the antimatter, support it, shield it, and control the vacuum to regulate the amount of power we want to take from it. There would still be some engineering details to be worked out such as the conversion of the released energy to electricity. But the design should be very similar to that of a nuclear reactor. I wonít go into the safety aspects of such a device, but at least there should be no hassle over waste disposal!
In addition to the energy production implications of having a chunk of antimatter available, nuclear and particle physicists would stand in a line several miles long for the opportunity of having it available for physics experiments. The forces that act between nuclear particles could be probed in important new ways if such stuff were available. We would be able to look at the problems of nuclear physics from a completely different perspective, and new and exciting results would surely follow.
Our major
problem is to find some antimatter: Where should we look? We already know
something about where antimatter cannot be found. Clearly there is no antimatter
on Earth. There has been some speculation that some of the large craters on the
surface of the Earth such as the Great Meteor Crater in
Could a planet or asteroid in the solar system be made of antimatter? It is very likely that there is no antimatter at all in the solar system. But how certain are we that there is none? We know that the Earth, the Moon, Venus, and Mars are made of ordinary matter because we or our space probes have made physical contact with them and were not annihilated. For the other planets we can answer this question using somewhat less direct data from gamma ray astronomy. An antimatter object of planetary size in the solar system would be the "brightest" gamma ray object in the sky, due to annihilation with protons from the solar wind (protons streaming from the sun). Our present rather crude measurements of the intensities of high energy gamma rays in space cannot be reconciled with any such "bright" objects. A smallish asteroid made of antimatter might exist in the solar system, if it was small enough or far enough away from Earth. An antimatter asteroid about the same distance from the Sun as Jupiter would have to have a diameter of less than about 150 km (94 miles) or we would have noticed its presence in gamma ray measurements performed in satellites or with high altitude balloons. As gamma ray measurements in space improve, we can expect more and more sensitivity to possible antimatter objects in the solar system. So if an antimatter something is out there in our solar system, we should know about it in a few years.
What about antimatter stars? Could Alpha Centauri or one of our other stellar neighbors be made of antimatter? Again we must rely on gamma ray measurements. "Empty" interstellar space is actually not completely empty. There is a certain amount of interstellar gas, mainly hydrogen, between the stars. An antimatter star would react with this gas by annihilation, producing gamma rays. If we assume that the density (and matter type) of gas in the vicinity of nearby stats is the same as that in the solar system, there can be no antistars within about 100 light years of Earth. Otherwise we would have seen the gamma rays from annihilation of the antistar with interstellar gas atoms. Further, the solar wind from such antistars should produce antiprotons, which should appear in cosmic rays near the Earth. No cosmic ray antiprotons (as of this writing) have ever been reported.
The same gamma ray information can be used in another way. Consider some "average" star in our galaxy, say 30,000 light years from Earth. If one such star were made of antimatter, its annihilation with interstellar gas would not produce enough gamma rays to come to our attention. However, if there were a sufficiently large number of such randomly distributed antistars, their combined gamma rays would reach the level of sensitivity of our detectors. How many such antistars would it take? About 10,000,000 antistars. In other words, our galaxy could contain 10 million antimatter stars. This seems to be a very large number, but it is only 1/10,000 of the total number of stars in our galaxy, which has a total "population" of about 100,000,000,000 stars.
Looking beyond our own galaxy to our galactic neighbors, our estimates become considerably more uncertain. This is because we know much less about the gaseous medium between galaxies. If the dilute gas between galaxies is not continuous, it could switch from diffuse hydrogen to diffuse antihydrogen somewhere between one galaxy and the next. On that basis, our sister galaxy M31, the Andromeda Nebula, could be made of antimatter. Similarly, the other minor galaxies in our Local Group might include some antigalaxies. The Virgo Cluster, the next galactic "town" from the Local Group, which contains some 20,000 galaxies, might be all or partly composed of antigalaxies. On the other hand, if there is a pervasive, continuous medium of hot dilute intergalactic gas throughout the region between galaxies (as has been suggested by some astrophysicists) then there can be little antimatter in our galactic neighborhood. Under those circumstances gamma ray data would imply that M31 could have at most one antistar per 1000 stars and the probability that nearby galaxies could be made of antimatter would be only 1/1000.
How could there be so little antimatter around? It implies that the universe is a rather unsymmetrical place, with all the matter in an untidy heap over here and perhaps the antimatter in another heap over there. Or maybe with no antimatter heaps at all. It seems a slapdash way to put together a universe!
Up to this point, our discussion of antimatter has been based on information that is presently available as a result of measurements already done and data already collected. Now let us turn to the future. We havenít found antimatter in nature up to now. This may mean there isnít any there, or it may mean that we will have to look harder if we are to find it. A first step would be to improve gamma ray measurements in space, both in their sensitivity and in their directionality. But further, let's consider what else we might be able to learn about the presence of antimatter in the universe, if we are clever enough in performing new types of measurements and obtaining new data. Before we can discuss such measurements, however, we must lay some background on the fundamental forces of nature and the fundamental symmetries of physical processes.
There are four fundamental forces in the universe that, as far as we know, account for all of the interactions within and between physical systems. These forces, in order of increasing strength, are: the gravitational force, the "weak" nuclear force, the electromagnetic force, and the "strong" nuclear force. The gravitational and electromagnetic forces are the ones with which we have the most familiarity, because they are "long range" forces obeying the well known inverse-square law. The other two forces, weak and strong, are more difficult to study because they are "short-range" forces and only reveal themselves when the interacting objects such as neutrons and protons are very close together indeed. The strong force holds nuclei together, and without it no nuclei would exist (and neither would we). The weak force is perhaps the most mysterious of the four. Its effects are not readily apparent, except in certain processes involving radioactive decay. However, if the weak force were suddenly to "turn off", the fusion reactions in the sun would cease. The sun would literally "go out." Physicists suspect that the weak force is linked in some way to the electromagnetic force, and this is presently the subject of very intensive investigation. The weak force exhibits very peculiar properties, some of which we will discuss below.
Imagine that with a very powerful microscope you are able to watch an "event" involving a physical process such as the interaction of a pair of fundamental particles, say an electron scattering from a proton. You are able to make high-speed movies of what you see. Now suppose that you make a similar film of the same process with antimatter particles (e.g., a positron scattered from an antiproton). You give these two films to a projectionist who will show the films while you watch. Unfortunately, your projectionist is very clumsy and inexperienced. He is quite capable of (1) mixing up the two films, (2) reversing the orientation of the film so that the image you see is the mirror image of the true process, (3) showing the film in reversed time sequence so that it runs backwards. Or he might make any combination of these mistakes at the same time. The question then is: Can you by watching the movie of the event and knowing some physics, tell if your inept projectionist has made one or more of the above mistakes? If, for instance, you can't tell the difference between an event viewed forward and backwards in time sequence, we would say that the process has "time-reversal invariance" or more simply, has T symmetry. Similarly, if we can it tell the matter film from the antimatter film of the same event, then the process that we are viewing is said to have "charge-conjugation invariance" or C-symmetry. If the normal film and its mirror image look the same, then the process that we are viewing is said to have "parity invariance" or P symmetry. If we canít tell that both (1) and (2) were done simultaneously, we say that the process has CP symmetry, and so forth. Fig. 3 shows schematically an atom of hydrogen as it appears under these various symmetry operations.
Note that in Fig. 3 we have used the convention that charges are reversed by the T (or time reversal) operation. The subtle arguments that lead to this result are due to Nobel Laureate Richard Feynman, who pointed out in the late 1970s that a positron (antimatter) can be described as an electron (matter) moving backwards in time.
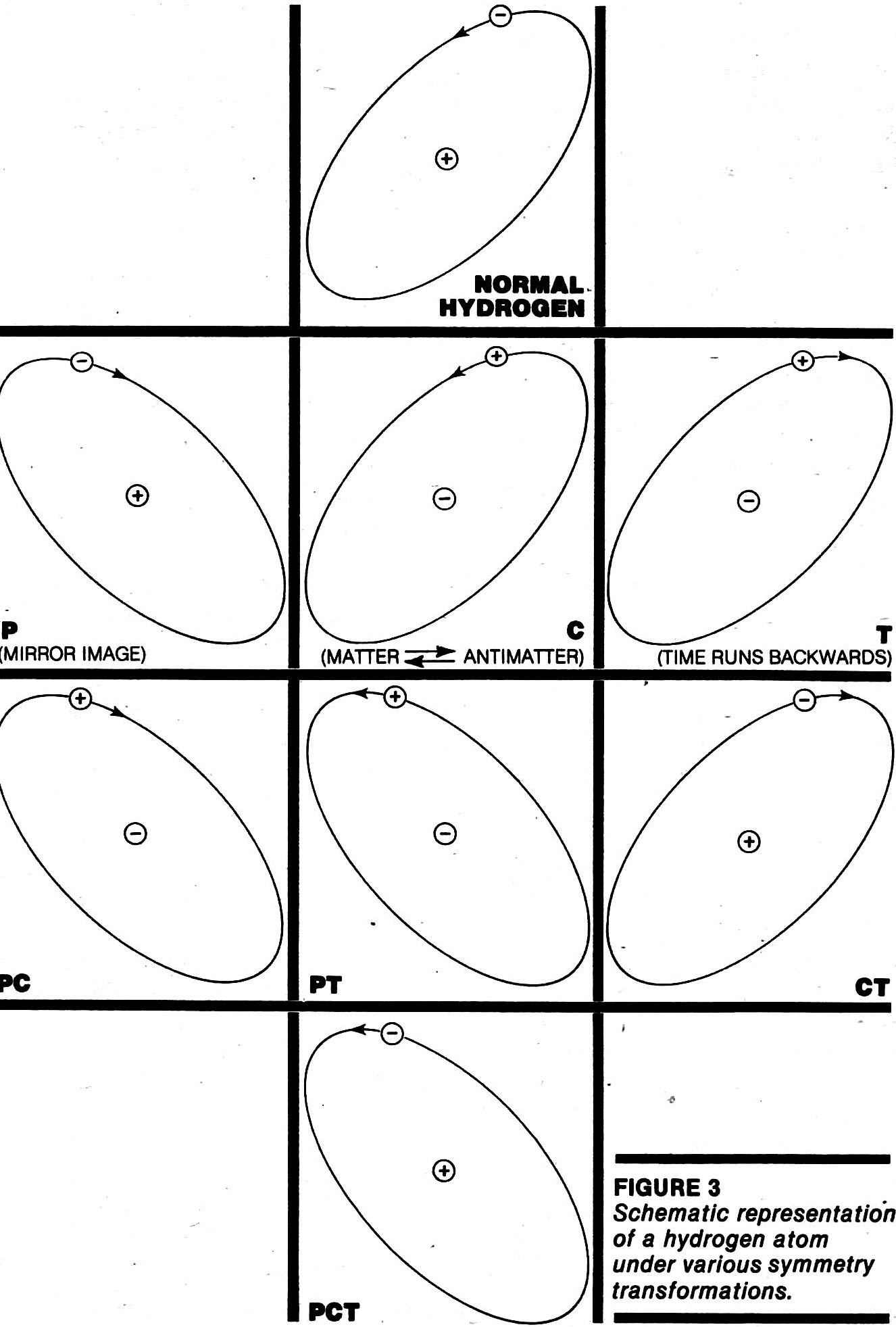
We should note that while microscopic processes may possess some of these symmetries, everyday processes clearly donít. All three symmetries are grossly violated in the events happening all around us. For example, our surroundings are all matter and no antimatter, which is a violation of C symmetry. Our bodies are not P symmetric, in that our hearts are on the left side and our mirror image would have a heart on the right. Time clearly runs forward and not backwards in a very non-T-symmetric way, so that a movie of an egg smashing on the floor is clearly distinguishable from the same movie run backwards (whereas, a movie of Ďan electron orbiting a proton is not). How symmetric microscopic process can combine to produce unsymmetric microscopic processes is a question that, at this writing, has not been satisfactorily answered in contemporary physics. (But that is the subject for another article.)
Up to 1957
the prevailing view in physics was that all microscopic physical processes
possessed C symmetry, P symmetry, and T symmetry. Then the roof fell in! It was
discovered that certain microscopic events involving the "weak" interaction
(for example, the kind of radioactivity called beta decay) showed gross
violations of P symmetry. They looked quite different in the mirror than they
did straight on. Subsequently it was found that these symmetry violations were
exactly reversed in antimatter systems, so that both C symmetry and P symmetry
were individually violated, but their effects cancelled in such a way that CP
symmetry was preserved. In other words, if our clumsy projectionist grabbed a
film of antimatter beta decay by mistake and then showed it mirror imaged we
would be unable to detect his mistakes and would think we were watching the
corresponding matter film shown properly. More recently, even this CP symmetry
has been found to be broken in the decay of the neutral
What does all of this have to do with our search for antimatter in the universe? lt has two kinds of implications. First, we believe that all microscopic processes possess CPT symmetry. It is therefore at least plausible that there might also be a kind of overall CPT symmetry that applies to the universe as a whole. The apparent dominance of matter over antimatter in the universe could, on this basis, be required in order to cancel the unsymmetric directionality of time that is apparent in all macroscopic processes and particularly in the expansion of the universe. Perhaps there is only matter in the universe so that time can have a unique direction. (Or perhaps not.)
My own contribution to the search for antimatter in the universe was to discover a second implication of these symmetry ideas. I realized that the violations of P-symmetry and C-symmetry in "weak" processes could be used as a handle for distinguishing matter for antimatter, and a colleague and I worked out a way in which this might be done even at interstellar or intergalactic distances. Stars start as almost all protons (in the form of hydrogen). They "burn" by a cycle of nuclear fusion, systematically converting more and more of their protons into neutrons. The "weak" processes of positron decay and electron capture are links in the chain of nuclear reactions that make up the fusion cycle. These weak processes violate P symmetry by emitting positrons and secondary gamma rays that have their spin axes pointing along their lines of flight. (Yes, gamma rays do "spin" as they move through space.) In an antimatter system (i.e., an antistar) the spin direction must reverse to preserve CP symmetry.
To understand this in more down-to earth terms, consider the manufacture of pistols. The barrels of pistols are rifled to spin the bullet as it emerges from the gun, but the manufacturers differ as to which direction of spin is used. In particular, pistols made by the Colt Co. spin their bullets counterclockwise when viewed by an observer looking down the gun barrel (admittedly a very bad vantage point). On the other hand, pistols made by Smith & Wesson spin their bullets clockwise. Thus if the good guys were shooting Colts while the bad guys were shooting S&Ws, a clever observer who found himself in the middle of a gunfight could tell the good guys from the bad guys by the spin of their bullets. To complete the analogy, the secondary gamma rays from the weak processes in matter stars spin like bullets from a Colt, while those from antistars spin like bullets from a S&W. In principle therefore, we can tell from observation of the spin of the secondary gamma rays from fusion whether a distant star is made of matter or of antimatter.
This is not as easy as it seems, for in a normal star the fusion reactions occur only very deep in the interior of the star, and the gamma rays can never escape. All stars, however, are not normal. Occasionally a massive star will burn all its hydrogen to helium, all its helium to carbon, all its carbon to silicon, and all its silicon to iron. Iron is the most "bound" nucleus, so the star cannot get more energy either by fusing two iron nuclei or by breaking one apart. Therefore, the star is literally "out of gas," because all of its nuclear fuel has been exhausted, its precarious equilibrium is lost, and it undergoes a catastrophic collapse and explosion called a supernova. For a brief time this star outshines the combined output of all the other stars in its galaxy, before it dwindles back to become a neutron star or a black hole. During its brief period of glory there are weak-force processes at work at its surface, liberating most of the observed energy and also making secondary gamma rays. If the material of the supernova is normal matter, these gamma rays will spin counterclockwise and if the supernova is made of antimatter they will spin clockwise. This is our clue.
The energy released in a supernova is so enormous that even if it occurs 3 million light years from Earth, there may be enough of these gamma rays to make it possible to determine their spin direction. The same trick can also be used on a cluster of galaxies such as the Virgo Cluster by collecting the radiation from a number of supernovae in a number of galaxies in the cluster, thus determining whether an object 60 million light-years away is made of antimatter.
Observational measurements such as these are far beyond what can presently be done. After the Space Shuttle begins routine flights, however, such measurements might be feasible. Determination of the spin direction of a gamma ray is done by scattering it from magnetized iron, and the sensitivity is not very high. A hypothetical space-mounted detector would have to be very large and might also have to be surrounded by shielding material such as lead, making for large payloads. The technology for the construction of such a detector is still under development by myself and others. In the context of gamma ray astronomy experiments of this complexity are still a "generation" or more away.
But the limits are being pushed back, day by day and year by year. Perhaps, in the days to come we will see a gamma ray "beacon" telling us that antimatter is being annihilated somewhere in our galaxy. Perhaps experiments to detect high energy neutrinos (which l hadnít the space to mention) will provide similar clues. Perhaps we will one day be able to learn from the death of an almost inconceivably distant star that a faraway galaxy is made of antimatter. Perhaps we can one day stand under the stars and point to the antimatter in the sky.
John G. Cramer's 2016 nonfiction book (Amazon gives it 5 stars) describing his transactional interpretation of quantum mechanics, The Quantum Handshake - Entanglement, Nonlocality, and Transactions, (Springer, January-2016) is available online as a hardcover or eBook at: http://www.springer.com/gp/book/9783319246406 or https://www.amazon.com/dp/3319246402.
SF Novels by John Cramer: Printed editions of John's hard SF novels Twistor and Einstein's Bridge are available from Amazon at https://www.amazon.com/Twistor-John-Cramer/dp/048680450X and https://www.amazon.com/EINSTEINS-BRIDGE-H-John-Cramer/dp/0380975106 . His new novel, Fermi's Question may be coming soon.
Alternate View Columns Online: Electronic reprints of 212 or more "The Alternate View" columns by John G. Cramer published in Analog between 1984 and the present are currently available online at: http://www.npl.washington.edu/av .
References:
"Observational Tests of Antimatter Cosmologies," G. Steigman, Annual Reviews of Astronomy and Astrophysics 14, 339, (1976).
"Distinguishing between Stars and Galaxies Composed of Matter and Antimatter Using Photon Helicity Detection," John G. Cramer and Wilfred J. Braithwaite, Physical Review Letters, 39, 1104, (1977).