In 1993 Elitzur and Vaidmann (EV) showed a surprised physics community that quantum mechanics permits the use of light to examine an object without a single photon of the light actually interacting with the object. The EV thought-experiment requires only the possibility of an interaction. More recently physicists at Los Alamos and Innsbruck have demonstrated the effect experimentally with an improved version of the EV scheme, have accomplished interaction-free imaging, and have boosted the efficiency of the process from 33% to over 75%.
The EV scheme was originally described as a thought experiment using a set of "photon-triggered bombs", and I'll use this bomb scenario to give the procedure more immediacy. Suppose that you are given a set of photon-triggered bombs housed in light-proof cases. There is a hole in each bomb through which light may pass. Some of the devices are "live" bombs, constructed so that when any single photon of light enters the hole, the bomb explodes. But there are also "dud" bombs that will allow any photon to pass completely through the hole and exit without an explosion. You are given the task of identifying as many devices as possible that are certain to be live bombs but that have not yet been detonated.
From the point of view of classical physics, this problem is impossible to solve. If all the devices are exposed to photons, the live bombs will all be destroyed and only the dud bombs will remain. However, the EV scheme employs the peculiarities of quantum mechanics to solve the problem. A signal can be derived from a quantum interferometer testing when there is only the possibility that the bomb will explode, even when it does not actually do so.
The apparatus that makes this test possible is called a Mach-Zehnder interferometer, a standard optical tool frequently used to measure the index of refraction of gases. The interferometer uses a 50%-50% beam splitter to divide incoming light into two beams. These beams are then deflected by 90° mirrors along paths that form a rectangle. They meet at a second beam splitter, which recombines them. The combined beams then go to one of two photon detectors. The diagram shows a Mach-Zehnder interferometer.
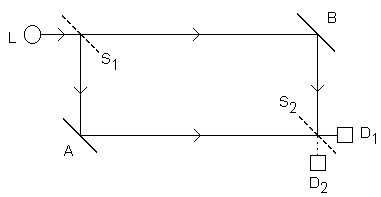
Suppose that we use a light source that can emit photons one at a time, on command. A photon emerges from the source and passes through the upper beam-splitter (upper dotted line), which has the characteristic that 50% of the time the photon will be reflected by 90° and 50% of the time it will be transmitted straight through. It may then travel to mirror A or to mirror B (solid lines) where it will be reflected by 90°. Along either path, the photon reaches the lower beam-splitter (lower dotted line), where it may again be transmitted or reflected, reaching either photon detector D1 or photon detector D2.
A Mach-Zehnder interferometer has the peculiarity that, if the paths between the beam-splitters have precisely the same path lengths, all photons will go to detector D1 and none will go to detector D2. The single photon must be treated as a wave that travels along both paths. After each beam-splitter, the emerging reflected wave is 90° out of phase with the emerging transmitted wave. This causes the waves at detector D1 to be in phase and to reinforce, while the waves at detector D2 will be 180° out of phase and will cancel.
Now suppose that we place an opaque object on the lower path after mirror A. It will block light waves along the lower path, insuring that all of the light arriving at the lower beam splitter had come along the upper path and been reflected by mirror B. In this case, there is no interference, and the lower beam splitter sends equal components of the incident wave into the two detectors.
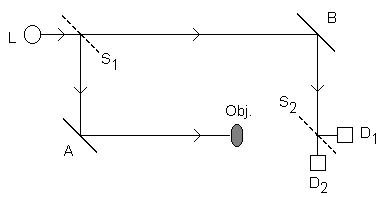
Thus, if we do the single photon measurement with no opaque object, we should detect the photon at D1 100% of the time. If we do the same measurement with the opaque object blocking the lower path, we should detect a photon at D1 25% of the time, a photon at D2 25% of the time, and detect no photon at all 50% of the time (because it was absorbed). In other words, the detection of a photon at D2 guarantees that an opaque object is blocking the lower path (but has not actually intercepted the photon). Detecting a photon at detector D1, on the other hand, gives no information on whether or not an object blocks the lower path.
One of the peculiarities of quantum mechanics, which distinguishes it from classical physics, is called the "collapse of the wave function". In a situation like the one described here, in which light waves that travel along two paths can interfere, that interference can take place only if we have no way of determining which path was taken. Any measurement that determines the path will "collapse" the wave function to that particular path, after which there can be no two-path interference.
Now, in a completely light-free laboratory, we place a photon-triggered bomb in the lower path, so that photons from the source will pass through the bomb's hole. If the bomb is live, then sending a single photon through its hole constitutes a "which-path" measurement. If the bomb explodes, we know that the photon took the lower path. If it does not explode, we know that the photon took the upper path. In either case, the wave function collapses to the indicated path. Therefore, if we detect a photon in detector D2 in this situation, it means that a photon did not take the lower path. In this case, we are guaranteed that the object in the lower path is a live bomb rather than a dud. Although no photon has reached it and it has not exploded, we have identified a live bomb. The EV scheme detects the possibility of a photon interaction with the bomb, even though no photon actually interacts with it. The photon that might have interacted with it has instead traveled along the upper path via mirror B.
If we perform this test on the set of photon-triggered bombs, 50% of the time the bomb will explode, 25% of the time we will receive an inconclusive D1 signal, and 25% of the time we will receive a D2 signal indicating an unexploded live bomb. If the test gives a D1 signal, we gain no information, but we can send in another photon and try again. After we have tried many times and always received a D2 signal, we may conclude that the lower path is open and that the bomb is a dud. The net result is that we will be able to identify one third of the live bombs while exploding two thirds of them, on average, and will identify all of the duds.
In 1998 a group of physicists from Los Alamos National Laboratory and Innsbruck, Austria reported that they had used an improved version of the AV technique to produce actual interaction-free high-resolution profiles of small objects (a knife-edge, a wire, a hair, an open slit). They used events in which no photons interact with the objects being "viewed" and plotted their profiles.
The same group, led by Paul Kwiat of Los Alamos, has devised a technique for improving the efficiency of the EV procedure, in effect reducing the number of exploded bombs to zero in the above example. They use another peculiarity of quantum mechanics associated with wave function collapse and called the quantum Zeno effect.
"The Problem of the Arrow" is one of the paradoxes proposed by the Greek philosopher Zeno of Elea. Imagine an arrow in flight. At some instant during its flight, it is in a fixed position. At another instant it is in another fixed position. In fact, at any instant, its position is always fixed. When, Zeno asked, does the arrow move? It is as if the act of examining the arrow's position prevents its motion.
At the end of the 1960s, several groups of theoretical physicists noticed that quantum mechanics contained the analog of Zeno's arrow paradox. Suppose you have a photon that is initially polarized horizontally (H) but that passes through an series of optical elements that progressively make small rotations of its polarization direction. Their cumulative effect is to rotate the photon's polarization to vertical (V).
However, quantum measurements are peculiar. We cannot simply measure a photon's polarization direction. Instead, we must pass it through a horizontal (H) polarizing filter and see if it survives. If so, it has H polarization, if not, it has V. Moreover, the measurement collapses the wave function, which resets the photon's polarization to be precisely H (or V).
Therefore, if after each rotator we place an H polarization filter, the photon is repeatedly reset to H and must emerge with H polarization. This is the quantum Zeno effect, the quantum equivalent of "a watched pot never boils". A "watched" (repeatedly measured) photon can't change its polarization, while a photon not watched can change its polarization freely.
Kwiat and his group applied the quantum Zeno effect to horizontally polarized photons that are recycled through one optical device that rotates the polarization orientation by a small angle. The photon proceeds to a splitter that transmits V polarization and reflects H polarization. Because there was only a tiny rotation in the polarization, the probability of transmission (V) is much weaker than that of reflection (H). This split is followed by mirrors and a device that recombines light on the H and V paths back into one beam.
The EV test is made by sending a single photon into the apparatus and intercepting the weak V beam path with an opaque object (the equivalent of passing it through the bomb's hole). The apparatus is arranged so the light is repeatedly cycled through, so there are many successive EV tests using the V component of the beam.
The net result is that if no object (or a dud bomb) is in the V path, there is no measurement and the recycled light beam after a number of passes will rotate from H to V polarization. However, if an opaque object (or live bomb) is in the V-beam, the survival of the photon constitutes a path measurement, and the photon polarization is repeatedly reset to the H polarization state. Therefore, final H polarization of the photon indicates the presence of an opaque object (or a live bomb) in the V path, while final V polarization of the photon indicates no opaque object (or a dud bomb) in the V path.
The group has shown that if the beam makes N passes through the system and the polarization rotator changes the polarization direction by an angle of 90°/N on each pass, the probability that the photon will interact with the opaque object (or the bomb will explode) is P(N) = 1 - [Cos(90°/N)]2N, a probability that decreases roughly as 1/N as the number of passes N is made large. For example, with 10 passes the probability of explosion is about 22%, with 100 passes it is 2.4%, and so on. The group has demonstrated the equivalent of these theoretical results (without using actual bombs) in the laboratory, achieving 75% efficiency and showing that at least 85% is feasible.
This amazing technique is still in its infancy, but it has interesting implications. It might be used on biological molecules that are light-sensitive and might be altered or destroyed by interaction with a photon, or on atomic systems where the act of measurement alters their properties. Another application is quantum computing. A non-interacting connection to a quantum computing element entangles the photon with the state of the system, permitting transfer of uncollapsed quantum information to another part of the system. Effectively, the quantum information is teleported from one part of the computer to another.
The prospect of making a measurement without an actual interaction should also have some interesting implications for hard SF. Analog writers take notice.
John G. Cramer's 2016 nonfiction book (Amazon gives it 5 stars) describing his transactional interpretation of quantum mechanics, The Quantum Handshake - Entanglement, Nonlocality, and Transactions, (Springer, January-2016) is available online as a hardcover or eBook at: http://www.springer.com/gp/book/9783319246406 or https://www.amazon.com/dp/3319246402.
SF Novels by John Cramer: Printed editions of John's hard SF novels Twistor and Einstein's Bridge are available from Amazon at https://www.amazon.com/Twistor-John-Cramer/dp/048680450X and https://www.amazon.com/EINSTEINS-BRIDGE-H-John-Cramer/dp/0380975106. His new novel, Fermi's Question may be coming soon.
Alternate View Columns Online: Electronic reprints of 212 or more "The Alternate View" columns by John G. Cramer published in Analog between 1984 and the present are currently available online at: http://www.npl.washington.edu/av .
Interaction-Free Measurements:
Elitzur and L. Vaidman, Foundations of Physics 23, 987 (1993).
Interaction-Free Imaging:
Andrew G. White, et al, Phys. Rev. A58, 605-608 (1998) and , preprint quant-ph/9803060 , LANL Archive, (26 April, 1998).
Quantum Zeno Interaction-Free Measurements:
P. G. Kwiat, et al, Phys. Rev. Letters (in press), preprint quant-ph/9909083, LANL Archive, (27 Sept., 1999); see also Scientific American, pp. 72-78 (Nov-1996), and http://p23.lanl.gov/Quantum/kwiat/ifm-folder/ifmtext.html