Albert Einstein argued that quantum mechanics was seriously flawed.  In 1927 at the 7^th Solvay Conference in Brussels, he proposed what we now call the Einstein Bubble Paradox.  It goes like this: An excited atom emits one photon of visible light.  The prevailing view of quantum mechanics says that this should produce a spherical wave function, expanding at lightspeed, like an inflating source-centered bubble.  The wave reaches a detector, and the photon is detected there.  Since the photon stops at the detector and deposits its energy there, it is assumed that its wave-function bubble should "pop", disappearing instantaneously over the entire spherical surface except at the detector.

Einstein asked how the bubble popped, i.e., how the remote parts of the wave function away from the detector "knew" that they should disappear at the instant of detection, and what mechanism governed their disappearance and prevented multiple photon detections.  (Note: Shahriar Afshar points out that this scenario is even more paradoxical than Einstein indicated.  The original atom recoils at the instant of photon emission in a direction opposite that of detection, and this recoil occurs well before the detection event occurs.  From the bubble viewpoint, this is strange because photon detection retroactively determines recoil direction, enforcing momentum conservation.)

At Solvay-7, Werner Heisenberg used his Copenhagen "knowledge" interpretation of quantum mechanics to answer Einstein's question.  The wave function, he said, is not a real physical object moving through space.  Instead, it is an encoded mathematical representation of the knowledge of some observer who is watching the process.  Until detection, the observer does not know the precise location of the emitted photon, so the wave function must be spread out over the whole expanding sphere to represent his ignorance.  However, at detection he learns the location of the photon, so the wave function "collapses" to the known location of the detector.  The other parts of the wave function must disappear because the observer's knowledge changes when he learns that the photon reached the detector and was absorbed.

Some of us find Heisenberg's explanation of the Bubble Paradox unsatisfactory.  The photon's wave function is the mathematical solution of the electromagnetic wave equation, a linear 2^nd order differential equation that relates space, time, energy, and momentum.  It has no discernable connection to "observers" or "knowledge".

My own transactional interpretation of quantum mechanics (TI) requires that the photon's expanding wave function (i.e., its offer wave) must continue to expand in all directions, even after a detection event, so that it can reach other possible photon absorbers and give them a fair shot at receiving the photon by the formation of a single advanced-retarded handshake connecting one of them to the source.  Further, the emission end of that completed handshake, forming at the atom at the instant of emission, implements momentum transfer and atom recoil.

Thus, we have two contrasting predictions: Heisenberg's knowledge interpretation requires the photon's expanding wave function to disappear when the observer learns the photon was detected elsewhere and absorbed.  The TI requires the wave function to continue expanding after the detection event.  We note that there are also many other interpretations of quantum mechanics, some predicting that Einstein's bubble pops, some predicting that it does not, and some so vague that there is no prediction.  However, up to now the physics community (including myself) has believed that there was no way of resolving this issue with an experiment that might falsify one group.

Recently that situation changed when Shahriar Afshar, whose paradigm-breaking work on two-slit interference was featured in my December-2004 Analog AV column, decided to find out experimentally whether the photon's wave function really disappears following detection.  After nearly two decades of experimental research and theoretical analysis, Afshar designed an experiment that may finally lift the veil on the behind-the-scenes workings of quantum mechanics.  Briefly, a single photon is produced, detected, and then tested to see if its "dark" wave still exists and can interfere with the overlapping coherent wave of a second photon emitted earlier.  This figure shows Afshar's new experimental setup in more detail.

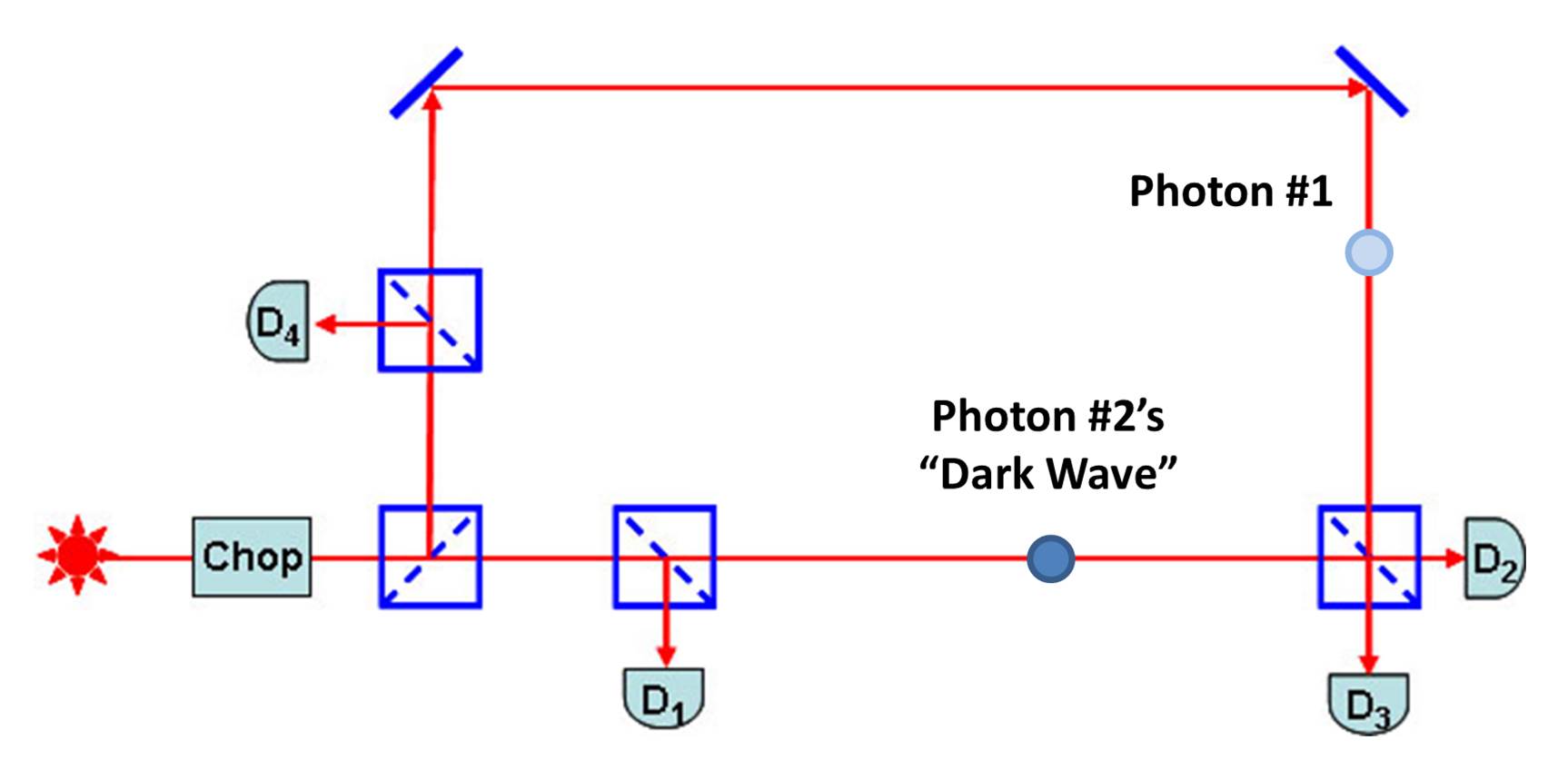
Afshar's Asymmetric Mach-Zehnder Interferometer

The source of photons is a weak long-coherence-length laser.  Following the laser is a chopper, where the continuous laser beam becomes a sequence of 10-50 ns pulses.  The laser's coherence length, several kilometers, ensures that the wave functions in successive pulses will be coherent and can interfere.  The laser pulses pass into the optical arrangement shown, which Afshar calls an "asymmetric Mach-Zehnder interferometer".

It is a rectangle of optical paths, with the laser pulse entering horizontally at the lower left corner of the rectangle, 50:50 beam splitters at the entrance and exit ports, and 90^o reflecting mirrors at the upper two corners.  In addition, there are "interrogator" beam splitters near the entrance port on both paths.  Single-photon detectors are placed as shown, with D₁ (short) and D₄ (long) at the interrogator splitters detecting photons on the short lower and long upper paths, and D₂ (bright) and D₃ (dark) at the interferometer's two exit-port outputs.

Since the upper and lower interferometer paths have quite different lengths, the height of the rectangle must be adjusted to sub-wavelength precision so that coherent light waves on the two paths arrive precisely in phase at the bright port (D₂) and 180^o out of phase at the dark port (D₃).

A pulse on the upper (longer) path requires a time Δt (~50 ns) more than a pulse on the lower (shorter) path to reach the exit ports.  The pulser is adjusted so that the generated pulses are spaced Dt apart, so that initial pulse #1 taking the upper path will arrive at the exit ports (D₂, D₃) at the same time as following pulse #2 taking the lower path.  Now Afshar looks for coincidences between D₁ detections of photon #2, electronically delayed, and D₂ or D₃ detections.

Suppose that photon #1 is emitted and at time Δt later has not been detected, and then photon #2 is emitted and detected by D₁.  The dark wave function of photon #2 (if it exists) proceeds on the lower path to the exit port.  If detection by D₁ of photon #2 causes its wave function to disappear on all paths, as Heisenberg knowledge requires, then photon #1's upper-path wave function should arrive at the exit port alone, with no wave interference from photon #2.  In that case, after the exit beam splitter photon #1 should have equal detection probabilities at D₂ and D₃.

However, if the detection of photon #2 by D₁ does not cause its lower-path wave function to disappear, then its dark wave function should arrive at the exit port simultaneously with the upper-path wave function of photon #1, and they should interfere.  In that case there will be constructive interference at detector D₂ and destructive interference at detector D₃, so all photons should be detected at D₂ and none at D₃.  Note that it is photon #2's energy that triggers this detection; photon #1's energy was spent earlier, and its interfering wave can only steer the second detection's location.

The experiment records D₁(delayed)+D₂ coincidences and D₁(delayed)+D₃ coincidences and compares their rates.  (Actually, multiple coincidences among all detectors are recorded as consistency checks.  For example, D₁+D₄ coincidences signal the unwanted presence of two photons in one pulse.)

Afshar made the laser intensity very weak to ensure with high probability that only one photon (or zero) was contained in every pulse.  This makes photon counting rates very low, and the accumulation of statistically significant coincidence data requires a time on the order of months.  At this writing, data are still coming in, but early indications, as presented by Afshar at the 2022 March Meeting of the American Physical Society, are that there is a definite preference for D₁+D₂ coincidences over D₁+D₃ coincidences, indicating that dark waves exist and can produce interference after their described photon has been detected.  Thus, wave function disappearance after local detection never occurs, indicating that the Heisenberg knowledge prediction is likely falsified.  If these results hold up after gathering a much larger data set, they suggest that the universe is awash with dark quantum waves (perhaps both retarded and advanced), heralding the new era of Dark Quantum Mechanics.

In most of physics, rival theories with differing predictions don't compete long because they must survive experimental tests.  The very large number of competing interpretations of quantum mechanics has been a problem-area of fundamental physics beginning in the 1920s, because testing and falsification have been absent.  Consequently, the burgeoning field of quantum interpretation has bordered on philosophy, and it has been largely ignored by mainstream physics.  The choice of quantum interpretations has become a matter of taste, opinion, whim, and academic politics.  A prominent experimental physicist friend once told me that he strongly supported the Copenhagen interpretation because he had done experiments at the Neils Bohr Institute in Copenhagen and his loyalty was there.

As it turns out, the physics community has been mistaken about the impossibility of testing interpretations.  As exemplified by Afshar's remarkable new experiment, if clever enough, one can do experiments that test the validity of quantum interpretations and probe the foundations of quantum mechanics.  There is evidence, growing stronger every day as data is collected, that dark waves do exist, that the quantum wave function does not disappear when the photon it describes is detected, and that Heisenberg and his disciples embracing the Copenhagen knowledge concept are not describing true quantum behavior.

Competing quantum interpretations can be divided into those popping Einstein's bubble (e.g., the Copenhagen interpretation), those not popping it (e.g., the TI), and those without predictions.  The former are in danger of being falsified.  It remains to be seen whether Afshar-2 will persuade the mainstream physics community to progress beyond defaulting to the Copenhagen interpretation.

Standard cosmology indicates that more than 95% of the mass-energy content of the universe is in the form of Dark Matter and Dark Energy.  It may soon be necessary however to add Afshar's newly discovered Dark Waves to our list of essential ingredients of the universe.

John G. Cramer's 2016 nonfiction book (Amazon gives it 5 stars) describing his transactional interpretation of quantum mechanics, The Quantum Handshake - Entanglement, Nonlocality, and Transactions, (Springer, January-2016) is available online as a hardcover or eBook at:  http://www.springer.com/gp/book/9783319246406 or https://www.amazon.com/dp/3319246402.

SF Novels by John Cramer:  Printed editions of John's hard SF novels Twistor and Einstein's Bridge are available from Amazon at https://www.amazon.com/Twistor-John-Cramer/dp/048680450X and https://www.amazon.com/EINSTEINS-BRIDGE-H-John-Cramer/dp/0380975106 .  His new novel, Fermi's Question is coming soon from Baen Books.

Alternate View Columns Online: Electronic reprints of 220 or more "The Alternate View" columns by John G. Cramer published in Analog between 1984 and the present are currently available online at: http://www.npl.washington.edu/av .

References:

Einstein's Bubble:

A. Einstein, in Electrons et Photons - Rapports et Discussions du Cinqui'ème Conseil dePhysique tenu, Bruxelles du 24 au 29 Octobre 1927 sous les Auspices de l'Institut International de Physique Solvay, Gauthier-Villars, Paris (1928).

M. Jammer, The Conceptual Development of Quantum Mechanics, McGraw-Hill,
New York, (1966).

Mach-Zehnder Interferometer:

L. Zehnder, Z. Instrumentenkunde 11, 275 (1891);

L. Mach, Z. Instrumentenkunde 12, 89 (1892).

The Afshar-2 Experiment

Shahriar S. Afshar, "Experimental Test of No-Collapse Quantum Mechanics: Are there Quantum 'Dark' States?", Bulletin of the American Physical Society, APS March Meeting (2022);
See also a video of the presentation at https://afsharlabs.org/afshar-2.

The Transactional Interpretation of Quantum Mechanics:

John G. Cramer, The Quantum Handshake - Entanglement, Nonlocality, and Transactions, Springer: Berlin/Heidelberg, Germany (2016); ISBN 978-3-319-24640-6; Section 6.2 discusses the Einstein Bubble Paradox.

John G. Cramer, "The Transactional Interpretation of Quantum Mechanics",
Reviews of Modern Physics 58, pp. 647–687 (1986) LINK.

Note:  The term "Dark Wave" was coined by Donald W. Glazer, who along with Jeremy Grantham has provided funding for Afshar's research.

Exit to the website.