|
|
|
|
Alternate View Column AV-81
Keywords: Alcubierre Warp Drive
FTL spacewarp solution Einstein's equations general relativity
Published in
the November-1996 issue of Analog Science Fiction & Fact
Magazine;
This column was written and submitted 4/15/96 and is
copyrighted ©1996 by John G. Cramer.
All rights reserved. No part may be
reproduced in any form without
the explicit permission of the author.
The theoretical physicist Miguel Alcubierre was born in Mexico City, where he lived until 1990 when he traveled to Cardiff in the UK to enter graduate school at the University of Wales. He received his PhD from that institution in 1993 for research in numerical general relativity, solving Einstein's gravitational equations with fast computers. He continues to work in this field, devising numerical techniques for describing the physics of orbiting black holes that spin down to collision.
Two years ago Alcubierre published a remarkable paper which grew from his work in general relativity, the current "standard model" for space-time and gravitation. His paper describes a very unusual solution to Einstein's equations of general relativity, described in the title as a "warp drive", and in the abstract as "a modification of space time in a way that allows a space ship to travel at an arbitrarily large speed". In this Alternate View column, I want to explore Alcubierre's work and its implications.
Let's start by considering the well-known velocity-of-light speed limit, as viewed by special relativity and by general relativity. In the context of special relativity, the speed of light is the absolute speed limit of the universe for any object having a real mass (i.e., everything but the semi-mythical tachyon), for two reasons. First, giving a fast object even more kinetic energy has the main effect of causing an increase in mass-energy rather than speed, with mass-energy going infinite as speed snuggles up to the velocity of light. By this mechanism, relativistic mass increase limits massive objects to sub-light velocities.
There is also a second faster than light (FTL) prohibition supplied by special relativity. Suppose a device like the "ansible" of LeGuin and Card were discovered that permitted faster-than-light or instantaneous communication. Special relativity is based in the treatment of all reference frames (i.e., coordinate system moving at some constant velocity) with perfect even-handedness and democracy. Therefore, FTL communication is implicitly ruled out by special relativity because it could be used to perform "sumultaneity tests" of the readings of separated clocks which would reveal the preferred or "true" reference frame of the universe. The existence of such a preferred frame is in conflict with special relativity.
General relativity treats special relativity as a restricted sub-theory that applies locally to any region of space sufficiently small that its curvature can be neglected. General relativity does not forbid faster-than-light travel or communication, but it does require that the local restrictions of special relativity must apply . In other words, light speed is the local speed limit, but the broader considerations of general relativity may provide an end-run way of circumventing this local statute. One example of this is a wormhole [see my AV columns in Analog, June-1989 and May-1990] connecting two widely separated locations in space, say five light-years apart. An object might take a few minutes to move with at low speed through the neck of a wormhole, observing the local speed-limit laws all the way. However, by transiting the wormhole the object has traveled five light years in a few minutes, producing an effective speed of a million times the velocity of light.
Another example of FTL in general relativity is the expansion of the universe itself. As the universe expands, new space is being created between any two separated objects. The objects may be at rest with respect to their local environment and with respect to the cosmic microwave background, but the distance between them may grow at a rate greater than the velocity of light. According to the standard model of cosmology, parts of the universe are receding from us at FTL speeds, and therefore are completely isolated from us. As the rate of expansion of the universe diminishes due to the pull of gravity, remote parts of the universe that have been out of light-speed contact with us since the Big Bang are coming over the lightspeed horizon and becoming newly visible to our region of the universe.
Alcubierre has proposed a way of beating the FTL speed limit that is somewhat like the expansion of the universe, but on a more local scale. He has developed a "metric" for general relativity, a mathematical representation of the curvature of space, that describes a region of flat space surrounded by a "warp" that propels it forward at any arbitrary velocity, including FTL speeds. Alcubierre's warp is constructed of hyperbolic tangent functions which create a very peculiar distortion of space at the edges of the flat-space volume. In effect, new space is rapidly being created (like an expanding universe) at the back side of the moving volume, and existing space is being annihilated (like a universe collapsing to a Big Crunch) at the front side of the moving volume. Thus, a space ship within the volume of the Alcubierre warp (and the volume itself) would be pushed forward by the expansion of space at its rear and the contraction of space in front. Here's a figure from Alcubierre's paper showing the curvature of space in the region of the travelling warp.
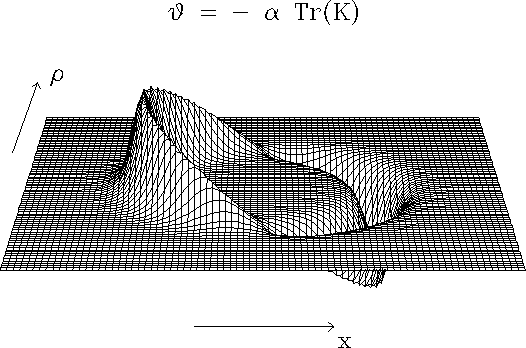
For those familiar with usual rules of special relativity, with its Lorentz contraction, mass increase, and time dilation, the Alcubierre warp metric has some rather peculiar aspects. Since a ship at the center of the moving volume of the metric is at rest with respect to locally flat space, there are no relativistic mass increase or time dilation effects. The on-board spaceship clock runs at the same speed as the clock of an external observer, and that observer will detect no increase in the mass of the moving ship, even when it travels at FTL speeds. Moreover, Alcubierre has shown that even when the ship is accelerating, it travels on a free-fall geodesic. In other words, a ship using the warp to accelerate and decelerate is always in free fall, and the crew would experience no accelerational gee-forces. Enormous tidal forces would be present near the edges of the flat-space volume because of the large space curvature there, but by suitable specification of the metric, these would be made very small within the volume occupied by the ship.
All of this, for those of us who would like to go to the stars without the annoying limitations imposed by special relativity, appears to be too good to be true. "What's the catch?" we ask. As it turns out, there are two "catches" in the Alcubierre warp drive scheme. The first is that, while his warp metric is a valid solution of Einstein's equations of general relativity, we have no idea how to produce such a distortion of space-time. Its implementation would require the imposition of radical curvature on extended regions of space. Within our present state of knowledge, the only way of producing curved space is by using mass, and the masses we have available for works of engineering lead to negligible space curvature. Moreover, even if we could do engineering with mini black holes (which have lots of curved space near their surfaces) it is not clear how an Alcubierre warp could be produced.
Alcubierre has also pointed out a more fundamental problem with his warp drive. General relativity provides a procedure for determining how much energy density (energy per unit volume) is implicit in a given metric (or curvature of space-time). He shows that the energy density is negative, rather large, and proportional to the square of the velocity with which the warp moves forward. This means that the weak, strong, and dominant energy conditions of general relativity are violated, which can be taken as arguments against the possibility of creating a working Alcubierre drive. Alcubierre, following the lead of wormhole theorists, argues that quantum field theory permits the existence of regions of negative energy density under special circumstances, and cites the Casimir effect as an example. Thus, the situation for the Alcubierre drive is similar to that of stable wormholes: they are solutions to the equations of general relativity, but one would need "exotic matter" with negative mass-energy to actually produce them, and we have none at the moment.
The possibilities for FTL travel or communication implicit in the Alcubierre drive raise the possibility of causality violations and "timelike loops", i.e., back-in-time communication and time travel. Alcubierre points out that his metric contains no such closed causal loops, and so is free of their paradoxes. However, he speculates that it would probably be possible to construct a metric similar to the one he presented which would contain such loops.
A scheme for converting FTL signaling to back-in-time signaling requires some gymnastics with moving reference frames to invert the time sequence of the "send" event and the "receive" event in a signal transmission. I described such a scheme in a recent column on quantum tunneling and FTL signaling [Analog, December-1995]. In the case of the` Alcubierre drive, this would probably require either externally moving the warp generating mechanism at near lightspeed velocities or embedding one warp within the flat-space region of another.
The implications of the Alcubierre warp drive for science fiction are fairly clear. If the theoretical and engineering problems outlined above could be overcome, we would have FTL travel, fully consistent with general relativity, that is reminiscent of the warp drives of the good old-time space operas. Remember, however, that using such a drive would undoubtedly require the manipulation of planet-scale quantities of energy (positive or negative). The user would also have to be very careful to avoid the tidal forces of the distorted-space region at the edges of the flat-space region containing the ship.
And there is also the question of writing the environmental impact statement. What would happen to external objects (space dust, rocks, other ships, asteroids, planets, ...) that happened to lie in the path of an Alcubierre ship and entered the region of distorted space-time at the leading edge of the warp, where space is rapidly being collapsed? The nuclei of any matter transiting that region would first experience enormous compressional forces, probably form a quark-gluon plasma reminiscent of the first microsecond of the Big Bang, and then explode in a flood of pi mesons and other fundamental particles when the compression forces were released, stealing energy from the warp field in the process.
A ship traveling in an Alcubierre space warp should be equipped with plenty of
radiation shielding. Perhaps that is not a problem, since the equations for
the metric and the energy density of the warp do not seem to depend on how much
mass is placed in the flat-space region which is given an FTL velocity.
Note (2/18/97): see also a recent
paper by Pfenning and Ford applying quantum limits to the
Alcubierre warp drive.
JGC
John G. Cramer's 2016 nonfiction book (Amazon gives it 5 stars) describing his transactional interpretation of quantum mechanics, The Quantum Handshake - Entanglement, Nonlocality, and Transactions, (Springer, January-2016) is available online as a hardcover or eBook at: http://www.springer.com/gp/book/9783319246406 or https://www.amazon.com/dp/3319246402.
SF Novels by John Cramer: Printed editions of John's hard SF novels Twistor and Einstein's Bridge are available from Amazon at https://www.amazon.com/Twistor-John-Cramer/dp/048680450X and https://www.amazon.com/EINSTEINS-BRIDGE-H-John-Cramer/dp/0380975106. His new novel, Fermi's Question may be coming soon.
Alternate View Columns Online: Electronic reprints of 212 or more "The Alternate View" columns by John G. Cramer published in Analog between 1984 and the present are currently available online at: http://www.npl.washington.edu/av .
References:
The Alcubierre Warp Drive:
Miguel Alcubierre, Classical and Quantum Gravity, v. 11, pp. L73-L77, (1994).General Relativity:
C. W. Misner, K. S. Thorne, and J. A. Wheeler, Gravitation, W.H. Freeman (1973).
|
|
|
|
This page was created by John G. Cramer on 7/12/1996 and revised on 2/18/1997 and 11/18/2014.