Short Range Tests of Newton's Inverse-Square Law
Motivation
Gravity poses one of the biggest mysteries in physics: why is it so weak when compared with all the other forces of nature? For instance, a small magnet suspended above a table can easily overcome the downward gravitational pull of the entire earth and pick up a nail.
Recently, an intriguing solution to this puzzle, involving "extra" space dimensions, has been suggested. String theory requires that there are 10 space dimensions, and it is usually assumed that 7 of these dimensions are curled up in very tiny regions, so small that they cannot be detected with foreseeable technology. The new idea, due to Arkani-Hamed, Dimopoulos and Dvali , is that the apparent weakness of gravity could be explained if gravity can "leak off" into the extra dimensions while everything else is confined to the usual 3 dimensions of length, width and height. In fact these extra dimensions could be as big as a millimeter and no experiment would have detected them! Gravity would be only way to "see" these extra dimensions, but the very weakness of gravity has meant that until recently there was no way to test the theory: no one had even been able to detect the gravitational attraction between two millimeter-sized objects, much less see if the force could be stronger than expected.
The value of the energy density of the cosmological constant (3 keV/cm^3), deduced from observations of distant Type-1A supernovae, corresponds to a length scale of about 0.1mm. S.R. Beane and others have noted that this energy density could produce deviations from Newtonian behavior just below the millimeter scale.
One particular model, proposed by Raman Sundrum to account for the cosmological constant problem, posits that the graviton is actually a "fat" particle which is unable to mediate the force of gravity at length scales smaller than itself. Under such a model, the force of gravity would appear to turn off at distances below the dark energy length scale.
Additionally, string theories predict the existence of new particles which could mediate as yet unseen interactions on this distance scale. Such particles include the dilaton and moduli found in theories containing supersymmetry (SUSY). These new interactions could also be observed in a short-range torsion balance experiment.
To date, the University of Washington Eöt-Wash group, led by physics professors Eric Adelberger, Blayne Heckel and Jens Gundlach, has tested the strength of gravity at distances down to 0.06 millimeters. Thus far no deviation from Newton's gravitational inverse-square law has been found in the short length-scale regime. The UW team remains actively engaged in measurements of ever increasing complexity and precision, consistently providing the best experimental limits of gravity-strength deviations available.
Regarding the many new gravitational theories being proposed by today's leading theorists: "We don't know if these ideas are right, but they are revolutionary," Adelberger said. "There would be profound consequences if the ideas are correct. The best way to find out is to devise a way to test gravity at even shorter distances. We are working on it."
The Eöt-Wash Short Range Experiment
Below is a cartoon of one of our initial experimental devices which illustrates the technique we employ to measure gravity at short length scales. The pendulum ring, with 10 small holes bored into it, hangs by a thin tungsten fiber (typically 20 microns thick) and acts as the dector mass. The rotating plate just below it, with 10 similar holes bored into it, acts as the drive mass providing gravitational pull on the pendulum that twists it back and forth 10 times for every revolution of the plate. The pendulum twist is measured by shining a laser beam off of a mirror mounted above the ring. The induced twist (torque) on the pendulum at varying separation distances is then compared to a detailed Newtonian calculation of the system.
Schematic Drawing of the Eöt-Wash Short-range Experiment
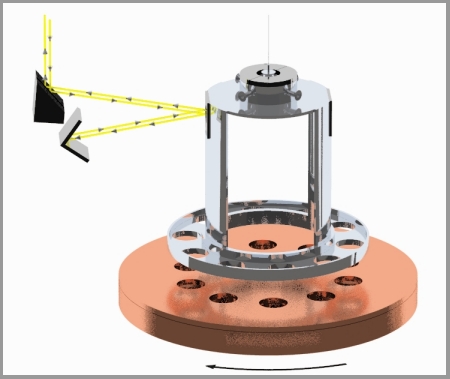
For many of our measurements, the rotating attractor situated just below the detector ring actually consists of 2 disks. The upper disk has holes identical to those in the detector ring. The lower, thicker attractor disk also has a similar hole pattern bored into it, but these larger holes are rotated compared to those in the upper disk, so that they lie halfway between the holes in the upper disk. If the inverse-square law is correct, the lower holes are designed such that they produce a twist on the ring that just cancels the twist induced by the upper disk. However, if gravity changes strength at short distances as the theories suggest, the twist induced by the lower disk, which is farther from the ring, will no longer cancel the twist from the upper disk and we will see a clear twist signal. The actual situation is a bit more complicated; for ordinary gravity the cancellation is exact only for one particular separation between the ring and the attractor, but the variation of the magnitude of the twist with changing separation between the ring and the disks provides a clear 'signature' for any new gravitational or other short-range phenomena.
As precaution against electrical forces interfering with the gravitational measuremnt, a grounded thin copper foil (not pictured above) is stretched between the detector ring and attractor disk, placing the two halves of the experiment in isolated Faraday cages. Also, all surfaces of the pendulum and foil are gold coated to minimize electrical patch effects.
| Eöt-Wash Short-range Pendulums | |
 |
Mark II short-range pendulum Used in 2002 experiment of Hoyle et al. In this design the detector mass is an aluminum ring with 10 holes. One can see the image of the pendulum ring in the mirror-like metal foil that separates the pendulum from the attractor. Read more about this experiment: arXiv:hep-ph/0011014v1 (This Link is a high-resolution TIF photo, 3.9Mb) |
 |
Mark VI short-range pendulum Used in 2006 experiment of Kapner et al. In this design the detector mass is a molybdenum ring with 42 holes, bored with a 21-fold symmetry. An added feature of this device is a continuous calibration signal provided by the gravitational interaction of the three aluminum spheres near the top of the pendulum with three brass spheres rotating outside the vacuum system. Read more about this experiment: arXiv:hep-ph/0611184v1 (This Link is a high-resolution TIF photo, 6.7Mb) |
 |
Wedge short-range pendulum Used in 2008 experiment of Cook et al. In this design the detector mass is a tungsten foil 0.05 millimeters thick with an 120-fold symmetric pattern of removed wedges. In addition, there is an 18-fold symmetric wedge pattern on the outside of the foil. These patterns are designed such that the 120-fold signal is highly sensitive to deviations from Newtonian gravity, whereas the 18-fold signal is highly insensitive to deviations. These two signals help to discriminate systematic effects from new physics. The foil is glued to a glass substrate to provide structural support. Measurements with the Wedge pendulum are currently underway. (This Link is a high-resolution JPG photo, 3.7Mb) |
Current Published Results
95% confidence level constraints on a Yukawa violation of the gravitational inverse-square law. The vertical axis represents the strength of a deviation relative to that of Newtonian gravity while the horizontal axis designates its characteristic range. The yellow region has been excluded. These results are detailed in "New Test of the Gravitational 1/r2 Law at Seperations down to 52 um,"
Recent Eöt-Wash Short Range Publications
"A Fourier-Bessel Test of the Gravitational Inverse-Square Law,” J.G.Lee's Dissertation (2020)
"New Test of the Gravitational 1/r2 Law at Seperations down to 52 um," J.G. Lee, E.G. Adelberger, T.S. Cook, S.M. Fleischer, B.R. Heckel. Physical Review Letters, (124), 101101 (2020)