| A Simple Composition Dipole | |
|
Torsion balance experiments in general measure some quantity by detecting a torque on a hanging pendulum; the torque is produced by some field interacting with a dipole or higher order moment. In some of our balances, we exploit a composition dipole to test for composition-dependent forces. For example, we constructed a dipole from Cu and Pb test bodies for our Rot-Wash experiment. |
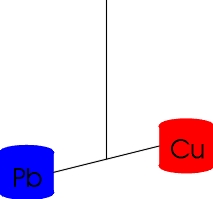 |
The pendulum sits in the field of an attractor; either the pendulum or the attractor mass is rotated so that an oscillating torque (easier to identify then a static torque) is produced.
One very nice feature of torsion balance experiments is that they are insensitive to slight differences in the masses or moment arms of the test bodies. Such differences will tilt the pendulum so that any torques that could be caused by the mass or moment arm differences cancel.
What does Eöt-Wash mean?
Our group's name is a pun on the name of a famous gravitational physicist, the Hungarian Count von Eötvös (pronounced something like ootvoosh with oo as in foot). Eötvös pioneered the use of torsion balances for testing the principle of equivalence, i.e. is gravitational mass (the mass entering in Newton's law of gravity F=G mm/r 2) exactly the same as inertial mass (the mass responsible for inertia in Newton's mechanical law F=ma). The suffix '-Wash' indicates that we are doing our gravity experiments at the University of Washington.
Experimental Motivation
At the heart of General Relativity lies the equivalence principle. In its simplest Newtonian form, it states that inertial mass and gravitational mass are the same thing, that is, gravity (as we know it) is the only fundamental force that couples exactly to mass, rather than to some kind of charge. The latter statement forms the basis of many of the experiments our group performs.
Many modern quantum theories of gravity predict violations of the equivalence principle, usually by Yukawa forces that couple differently to different chemical elements. Predictions for the range and strength of such violations have varied a great deal, and so we have performed torsion balance tests of the equivalence principle designed to be sensitive to ranges as small as a centimeter.
Recently new predictions about possible new behavior of gravity at short length scales have appeared. Instead of violating the equivalence principle, these theories predict violations of the gravitational inverse-square law. These suggest that gravity, and only gravity, penetrates extra, compact dimensions. These interesting hypotheses have been offered as solutions to the hierarchy problem (gravity is extremely weak when compared with any other force), and are the basis for our latest, short-range experiment.
You're encouraged to peruse our front page, results, experiments, and, of course, our publications to come to a greater understanding of why we're excited about our work!
How does a Torsion Balance work so well?
Torsion balances have the unique feature that they are sensitive to the angle between the forces on their test bodies. In particular, if the the forces on the test bodies are parallel there will be no torque on the balance, even if the forces have different magnitudes. (This explains why torsion balances can be used to make measurements at the part in 1013 level even though no part of the balance is itself good to that precision.)
To see this, consider the simple torsion pendulum, shown below, that contains 2 test bodies held by a massless frame hanging from a fine fiber.The vector connecting the test bodies is r=r1-r2.
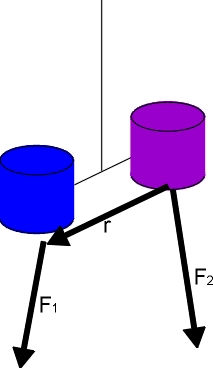 |
The torque on the torsion pendulum produced by forces acting on two test bodies is:
T = r1 x F1 + r2 x F2
The fiber must hang along the vector F1 + F2.Otherwise, the net force on the pendulum could not be zero, and it could never be at rest. The component of the torque parallel to the fiber will twist the fiber. This component is proportional to
(F1 + F2)·T = r1 · F1 x (F1 + F2) + r2 · F2 x (F1 + F2).
(F1 + F2)·T = r1 · F1 x F2 - r2 · F1 x F2.
where we used rules about scalar triple products to rearrange the expression.
Then,
T = (r · F1 x F2) /(F1 + F2).
So, the torque on the fiber depends on the angle between the two forces. There is no torque unless there is a non-zero angle between the forces, so torsion balance experiments are null experiments that detect any non-parallelism of the forces on the test bodies.
In our experiments, we test the equivalence principle by comparing the ratio of gravitational forces on the test bodies to the ratio of inertial forces on the test bodies caused by the rotation of the earth. If the ratios aren't the same, then the inertial force and gravity are not coupling to the same thing in the test bodies. And, because the ratios of the components of one vector to those ofthe other aren't the same, there will be an angle between the forces which wewill see as a torque on the torsion fiber.
Now, in the real world there are complications. We tacitly assumed that the gravitational field was uniform. In a non-uniform field, even if the test bodies are identical, there will be an angle between the forces on the test bodies. We must make the local gravitational field free from gradients, and we must make the pendulum as insensitive to gradients as possible.
Where we experiment
Our experiments are housed within the Center for Experimental Nuclear Physics and Astrophysics (CENPA).
Pictures of our labs are forthcoming. Explore the links on the left to learn more about our experiments themselves!